I. Introduction▲
Algorithme
implémentation
Optimisation
Présentation de l'algorithmique géométrique Computational Geometry
Deux dimensions
II. Présentation de la triangulation de Delaunay▲
Voronoi
Enveloppe convexe
Plus proche voisin
Eléments finis
Modélisation de terrains et de surfaces.
III. Algorithme incrémental▲
http://en.wikipedia.org/wiki/Bowyer%E2%80%93Watson_algorithm
Principes
Déroulement visuel
http://www.photosnack.com/YahikoUzumaki2/incremental-delaunay-triangulation.html
Etape 1) Initialisation
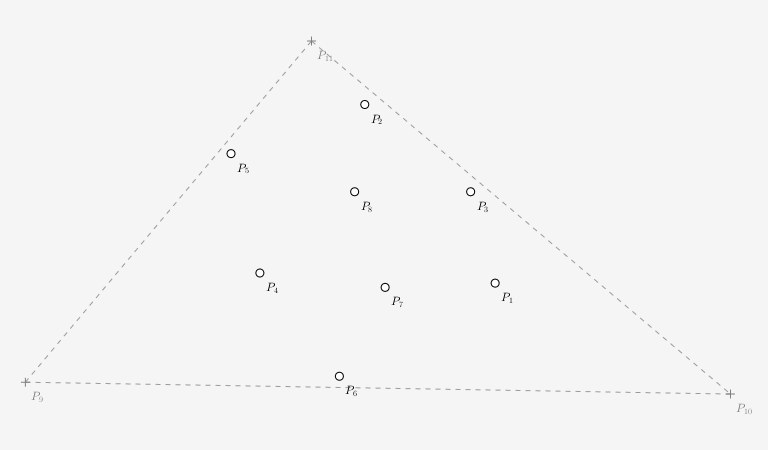
On initialise l'algorithme avec un triangle fictif, englobant l'ensemble des points à trianguler. Ce triangle étant par nature une triangulation de Delaunay pour ses trois poins, ceci va nous permettre d'utiliser l'algorithme incrémental qui s'applique sur une triangulation de Delaunay pré-existante.
L'important étant que cette initialisation fournit une triangulation de démarrage avec les trois points du triangle fictif.
Triangle fictif englobant 8 points à trianguler
Etape 2) Insertion d'un point
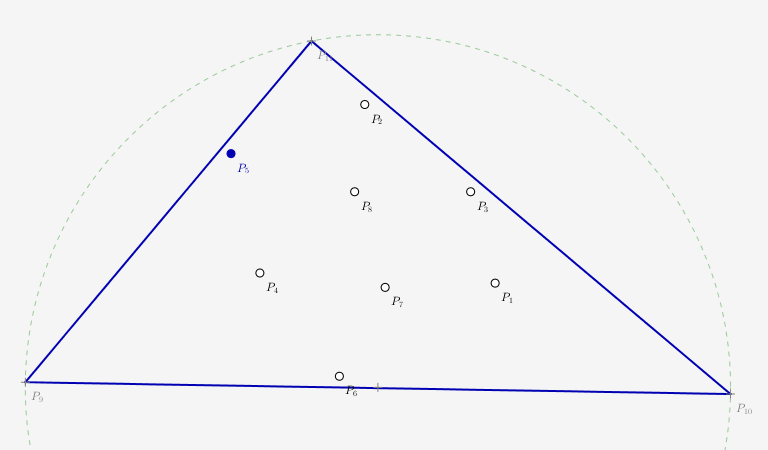
À la triangulation existante, on ajoute un point de notre ensemble à trianguler. Il peut être choisi au hasard même si selon la topologie il peut être judicieux d'ordonner l'insertion des points selon certains critères.
Une fois le point sélectionné, on recherche l'ensemble des triangles dont le cercle circonscrit contient strictement le point concerné.
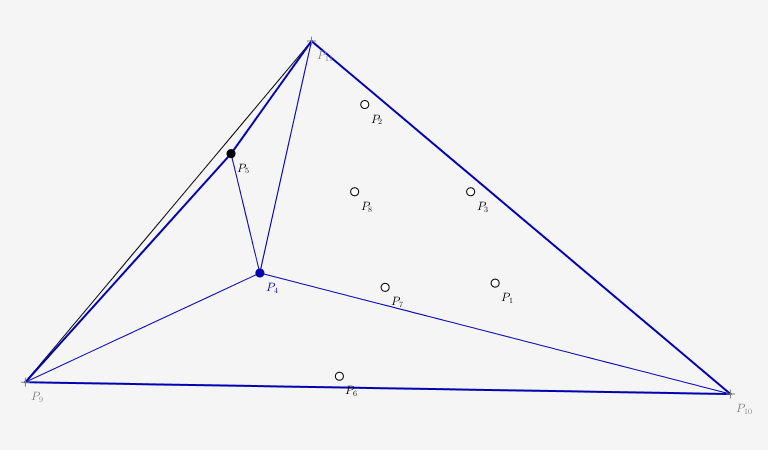
Insertion du point p5
Etape 3) Suppression et création de triangles
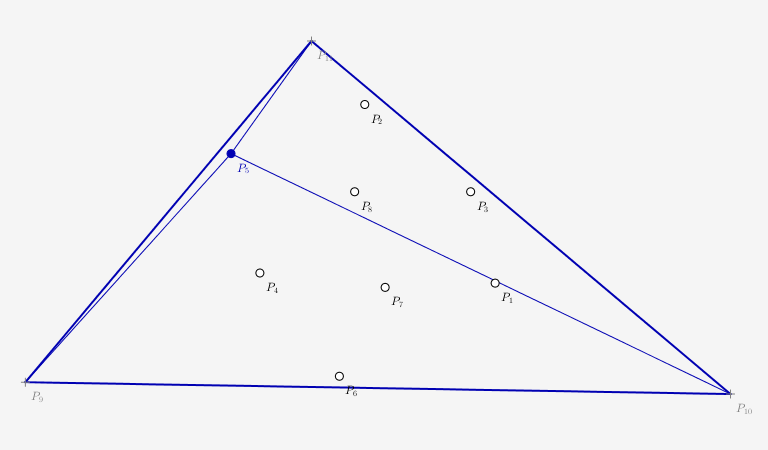
Les triangles dont le cercle circonscrit contiennent le nouveau point inséré ne vérifient plus la condition de Delaunay. On dit aussi que ces triangles sont illégaux. Ils doivent par conséquent être supprimés de la triangulation en cours. Les autres triangles dont le cercle circonscrit ne contient pas le nouveau point inséré sont conservés dans la triangulation en cours.
L'ensemble de ces triangles illégaux forment un polygone connexe dont le contour, qu'on nommera frontière, va nous servir à construire les nouveaux triangles.
Les triangles illégaux sont donc supprimés, et on crée autant de nouveaux triangles qu'il y a de segments formant le contour, chaque segment du contour servant de côté à chaque nouveau triangle.
Suppression du triangle illégal (p9, p10, 111) puis création des triangles (p11, p9, p5), (p9, p10, p5) et (p10, p11, p5).
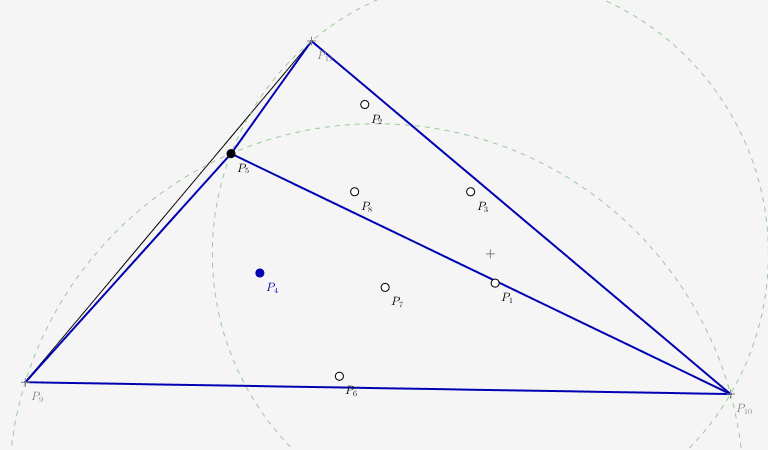
Tant qu'il reste des points à insérer, on recommence le procéder à l'étape 2). Ce n'est que lorsqu'il ne reste plus aucun point à traiter qu'on peut passer à la finalisation.
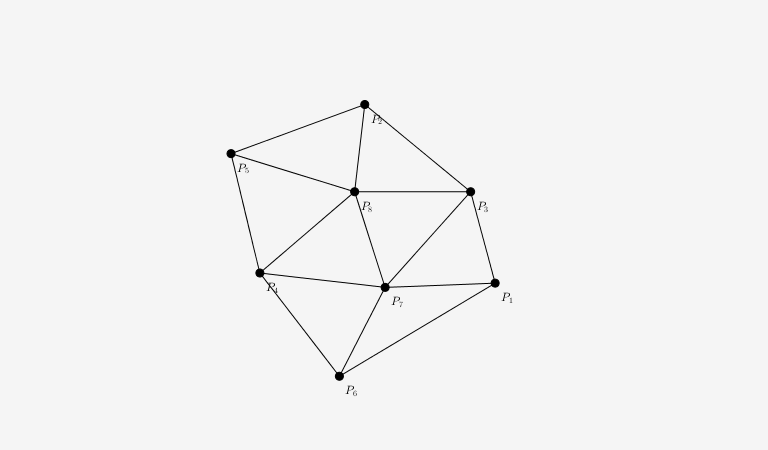
Etape 4) Finalisation
Cette étape consiste simplement à nettoyer la triangulation des triangles contenant les points du triangle fictif englobant du départ.
Une fois la triangulation débarrassée de ces triangles désormais encombrant, nous avons notre triangulation finale respectant la condition de Delaunay.
IV. Modélisation géométrique▲
IV-A. Structures de données▲
Point
x : nombre
y : nombre
Segment
a : Point
b : Point
Cercle
centre: Point
rayon : nombre
Triangle
sommets : liste de 3 Points
circonscrit : Cercle
Le terme de « triangulation » désignera une liste de Triangles.
IV-B. Opérations▲
creerTriangleEnglobant
entrée : liste de points P.
sortie : Triangle t tel que n'importe quel point pi de P est à l'intérieur de t.
calculerCercleCirconscrit
entrée : Triangle t.
sortie : Cercle c tel que c est le cercle circonscrit de t.
obtenirCotesTriangle
entrée : Triangle t.
sortie : liste de Segments S tel que S soit égal à l'ensemble des côtés de t.
supprimerCotesCommuns
entrée : liste de Segments S.
sortie : liste de Segments S' tel que s'il existe s1 et s2 de S avec s1 = s2, alors s1 et s2 n'appartiennent pas à S'.
obtenirFrontiere
entrée : liste de Triangles T
sortie : liste de Segments S tel que s'il existe s1 et s2 côtés de T avec s1 = s2, alors s1 et s2 n'appartiennent pas à S'.
rechercherTrianglesConteneurs
entrée : Point p, liste de Triangles T.
sortie : liste de Triangle T' et T'' tel que pour chaque t' élément de T' on a p à l'intérieur (bord exclu) du cercle circonscrit de t'.
ajouterPoint
entrée : Point p, liste de Triangles T.
sortie : liste de Triangles T' tel que T' contient l'ensemble des points de T ajouté de p et où p est le sommet d'au moins un triangle t' de T'.
trianguler
entrée : liste de Points P.
sortie : liste de Triangles T tel que T est la triangulation de Delaunay de P.
IV-C. Pseudo-code▲
Fonction trianguler(P)
// Initialisation
Soit t0 = creerTriangleEnglobant(P)
Soit T = [ t0 ]
// Boucle sur les Points
Pour chaque Point p de P
ajouterPoint(p, T)
Fin pour
// Suppression du triangle englobant
Pour chaque Point p de t0.sommets
Soit I l'ensemble des triangles de T ayant p comme sommet.
T = T - I
Fin pour
retourne T
Fin trianguler
Fonction ajouterPoint(p, T)
// Suppression des triangles dont le cercle circonscrit contient p
Soit D = rechercherTrianglesConteneurs(p, T)
Pour chaque Triangle t de D
T = T - t
Fin pour
// Création de nouveaux triangles vérifiant la condition de Delaunay
Soit F = obtenirFrontiere(D)
Pour chaque Segment s de F
Soit t = Triangle(s.a, s.b, p)
T = T + [t]
Fin pour
Fin ajouterPoint
V. Implémentation en TypeScript▲
Code source
Visualisation
VI. Optimisations▲
Cercle circonscrit
Balayage
Adjacence
VII. Conclusion▲
Flip
balayage
diviser pour régner
généralisation en dimension supérieure
géométrie non-euclidienne
VII-A. Remerciements▲
VIII. Références▲
Bowyer