Le but de l'interpolation est de compléter un ensemble de valeurs données à des positions données avec de nouvelles valeurs plausibles, en cohérence avec les valeurs déjà existantes.

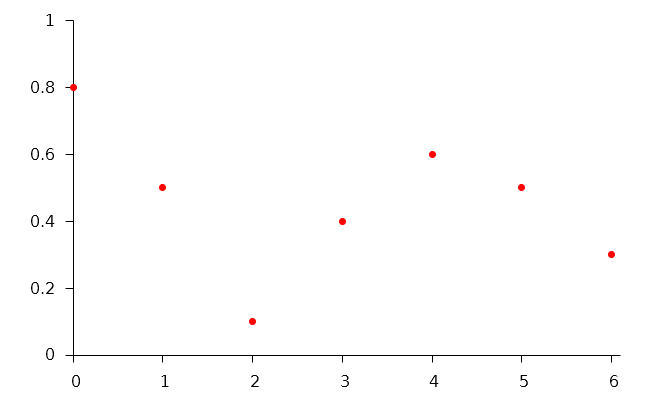
L'ensemble des positions et des valeurs initiales pourraient être représentées par des points sur un repère orthonormé en deux dimensions comme ci-dessous :

En général, les points peuvent ne pas être espacés à intervalle régulier. Cependant, dans la pratique, les systèmes de mesure ou les algorithmes informatiques génèrent très souvent des données réparties à intervalle régulier. C'est pourquoi, pour des raisons de simplicité dans les explications et dans l'implémentation, nous ne considérerons que cette situation.

Une interpolation pourrait consister ici à déterminer pour une position donnée, par exemple kitxmlcodeinlinelatexdvpx=0.5finkitxmlcodeinlinelatexdvp, une valeur en kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp.

Intuitivement, compte-tenu des points initiaux de la figure 1, une valeur trop élevée comme kitxmlcodeinlinelatexdvpy=10finkitxmlcodeinlinelatexdvp, ou bien négative ne serait pas cohérente. Il nous faut donc une règle nous permettant de calculer les différentes valeurs en kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp en fonction de kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp assurant la cohérence de l'ensemble des valeurs.

Une définition un peu plus rigoureuse serait de dire que l'interpolation consiste à déterminer une fonction, simple de préférence, dont la courbe représentative passe par les points initiaux. Cette fonction est appelée fonction interpolatrice ou interpolant. La fonction interpolatrice a pour objet de se rapprocher d'une fonction inconnue dont la courbe représentative passerait elle aussi par les points initiaux.

Si on note kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp la fonction interpolatrice, alors elle doit vérifier kitxmlcodeinlinelatexdvpf(x_i)=y_ifinkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpy_ifinkitxmlcodeinlinelatexdvp correspondent respectivement aux positions et aux valeurs initiales.

Les points initiaux indiqués plus haut serviront de jeu d'exemple pour l'ensemble de ce document. Ceci afin de faciliter la compréhension et la comparaison entre les techniques.

L'interpolation est l'un des problèmes fondamentaux de l'analyse numérique avec des applications aussi bien en ingénierie avec par exemple la méthode des éléments finis, qu'en statistique et aussi en informatique, notamment en infographie (Computer Graphics).

À noter que l'interpolation est différente de l'approximation qui elle n'impose pas à la courbe représentative de la fonction approchante de passer par tous les points donnés.