L'interpolation arrondie est également connue comme l'interpolation du plus proche voisin (nearest neighbour). Le principe est très simple puisqu'il s'agit de choisir pour une abscisse donnée, la valeur en kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp du point le plus proche. Cela revient à définir une fonction constante par morceaux, communément appelée fonction en escalier.

Voici une implémentation de cette méthode en TypeScript pour une interpolation entre deux points :

function neighbour(y0: number, y1: number, t: number): number {
    return (t < 0.5 ? y0 : y1);
}

La fonction neighbour() ainsi définie prend trois paramètres. Les paramètres y0 et y1 et correspondent aux valeurs initiales. Le paramètre t correspond à la position relative de la valeur à interpoler. Si kitxmlcodeinlinelatexdvp0 \leqslant t < 0.5finkitxmlcodeinlinelatexdvp, alors la fonction neighbour() retournera y0. Si kitxmlcodeinlinelatexdvp0.5 \leqslant t \leqslant 1finkitxmlcodeinlinelatexdvp, alors la fonction neighbour() retournera y1.

Pour avoir l'interpolation en kitxmlcodeinlinelatexdvpx=3.1finkitxmlcodeinlinelatexdvp, nous devons renseigner les valeurs en kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpx_0=3finkitxmlcodeinlinelatexdvp (kitxmlcodeinlinelatexdvpy_0=0.4finkitxmlcodeinlinelatexdvp) et pour kitxmlcodeinlinelatexdvpx_1=4finkitxmlcodeinlinelatexdvp (kitxmlcodeinlinelatexdvpy_1=0.6finkitxmlcodeinlinelatexdvp). Pour la valeur du paramètre t cela revient et considérer un nouveau repère ayant pour origine (kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp ; 0). Dans ce nouveau repère, kitxmlcodeinlinelatexdvpx=0.1finkitxmlcodeinlinelatexdvp. Le code correspondant serait :

y = neighbour(0.4, 0.6, 0.1);
// y === 0.4

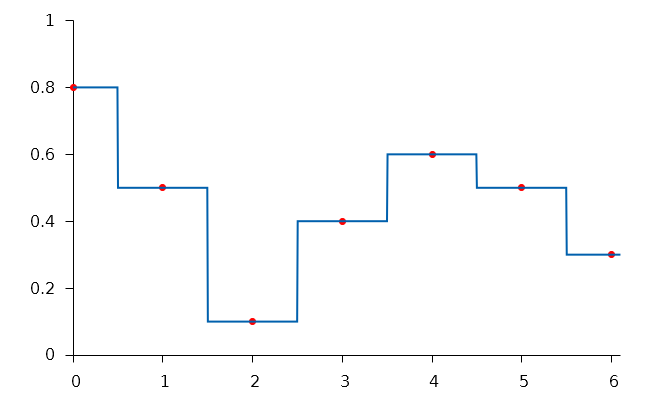
Il est facile de voir qu'en appliquant cette fonction à chaque paire de points successifs, en faisant varier à chaque fois t entre 0 et 1, on obtient une courbe en escalier comme celle de la figure 2.

Le coût en calcul de la fonction neighbour() est très faible puisqu'elle ne comporte en tout et pour tout qu'un seul test logique. C'est probablement l'interpolation la plus simple et la plus rapide. Si l'intervalle entre deux valeurs initiales est faible, réduisant d'autant l'erreur potentielle d'interpolation, cette méthode peut être une option tout à fait pertinente. Elle est d'ailleurs régulièrement utilisée en animation 3D au niveau du rendu des textures (texture filtering).

Cependant, il apparaît qu'une telle courbe en escalier n'est pas des plus « esthétique » et peut ne pas être en cohérence avec les valeurs attendues. L'interpolation linéaire est une étape vers plus de vraisemblance.