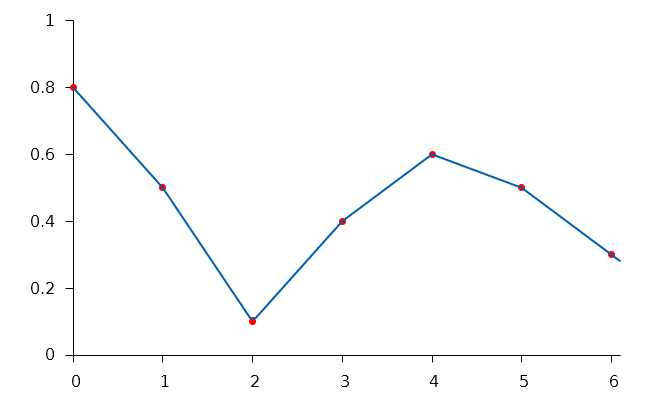
L'interpolation linéaire remplace les fonctions constantes par morceaux par des fonctions linéaires (en toute rigueur, affines) dont la courbe représentative est composée de segments de droites (dans le cas d'une courbe représentative en deux dimensions).

Pour rappel, une droite a pour équation kitxmlcodeinlinelatexdvpy=a\,x+bfinkitxmlcodeinlinelatexdvp tels que kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp sont des nombres réels où kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp est le coefficient directeur (ou encore la pente) et kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp est l'ordonnée à l'origine.

Pour obtenir une valeur de kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp entre deux points en fonction de kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp, il faut donc déterminer les valeurs de kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp.

Cela revient à résoudre un système linéaire de deux équations à deux inconnues.

Sur l'intervalle [0 ; 1] on a :

function lerp(y0: number, y1: number, t: number): number {
  return (y1 - y0) * t + y0;
}

Tout comme la fonction neighbour() vue précédemment dans le cadre de l'interpolation arrondie, la fonction lerp() prend les trois mêmes paramètres.

Pour avoir l'interpolation en kitxmlcodeinlinelatexdvpx=3.1finkitxmlcodeinlinelatexdvp, le code correspondant serait :

var y = lerp(0.4, 0.6, 0.1);
// y === 0.42000000000000004

Bien que théoriquement juste, le code de l'interpolation linéaire fourni précédemment ne garanti pas les relations lerp(y0, y1, 0) === y0 et lerp(y0, y1, 1) === y1 qui définissent le principe de base de l'interpolation : kitxmlcodeinlinelatexdvpf(x_i)=y_ifinkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvp(x_i, y_i)finkitxmlcodeinlinelatexdvp est un point initialement donné.

À cause de la représentation même des nombres décimaux au sein de la machine, l'addition ou la soustraction entre deux nombres ayant un écart important d'ordre de grandeur, peut entraîner des aberrations de calcul. Ce n'est donc pas un bug lié au langage TypeScript. Pour s'en convaincre, avec l'implémentation précédente, l'appel lerp(10e20, 0.6, 1) renvoie 0 au lieu de la valeur attendue qui est 0.6.

Pour remédier à ce problème d'implémentation, il est possible de reformuler la fonction lerp() de la sorte :

function lerp(y0: number, y1: number, t: number): number {
  return y0 * (1.0 - t) + y1 * t;
}

L'interpolation linéaire est utilisée dans d'innombrables applications de par sa simplicité et sa rapidité. De plus, par rapport à l'interpolation arrondie, elle améliore significativement la vraisemblance des valeurs interpolées.

Si on considère sa forme stable, cette méthode ne met en jeu que deux multiplications et deux additions. Ceci peut s'avérer plus performant même que le test logique de l'interpolation arrondie sur certaines implémentations et plate-formes.

Néanmoins, l'interpolation linéaire a ses défauts, notamment les « discontinuités » présentes aux points initiaux, peu naturelles. Pour être plus exact, la dérivée première de l'interpolation linéaire par morceau n'est pas continue.

Pour modéliser plus précisément de nombreux phénomènes du monde réel, il peut être souhaitable de rendre le résultat plus lisse. Pour cela, il existe plusieurs techniques.