Le but de l'interpolation cosinusoïdale est de lisser les angles formés par les segments de droite de l'interpolation linéaire en recourant à un changement de variable.

Plutôt que d'injecter directement la variable kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp dans la fonction lerp(), l'idée est de « ralentir » la variation de kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp au voisinage des points initiaux, adoucissant ainsi la courbe représentative résultante. L'essentiel étant que pour tout kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp dans l'intervalle [0 ; 1], la nouvelle variable soit également dans l'intervalle [0 ; 1].

Cela peut être obtenu en remaniant légèrement la fonction cosinus. En ne considérant que sa demi-période croissante et en la mettant à l'échelle pour que l'image soit comprise dans l'intervalle [0 ; 1], on peut obtenir une nouvelle variable kitxmlcodeinlinelatexdvpufinkitxmlcodeinlinelatexdvp exprimée en fonction de kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp dont les variations ralentissent à proximité des points initiaux.

L'implémentation de l'interpolation cosinusoïdale fait donc appel à l'interpolation linéaire via la fonction lerp() après avoir transformé la variable kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp fournie en paramètre avec la fonction cosinus que nous venons de voir.

function cosine(y0: number, y1: number, t: number): number {
  var u = (1.0 - Math.cos(t * Math.PI)) * 0.5;
  return lerp(y0, y1, u);
}

Cette nouvelle fonction cosine() prend les mêmes paramètres que les fonctions précédentes. Le lecteur pourra donc se reporter aux précédents chapitres pour avoir plus d'information sur ces paramètres.

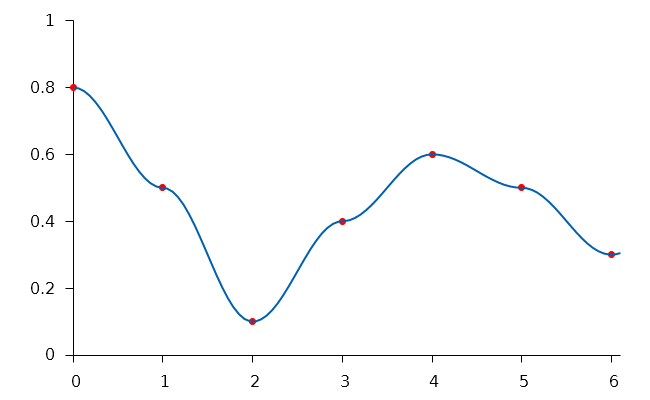
La courbe représentative de cette nouvelle fonction est assez satisfaisante dans la mesure où elle est relativement lisse même si elle présente quelques artefacts au niveau de certaines jonctions.

Cependant, si la fonction cosine() est appelée intensivement, cela peut poser des soucis de performance, à cause du coût relativement élevé de la fonction cosinus.

C'est pourquoi d'autres changements de variable que celui que nous venons de présenter ont été mis au point.