Pour améliorer les performances ou pour appliquer un autre type de transition entre deux points initiaux à interpoler, il est possible de faire appel à d'autres changements de variable que celui de la fonction cosinus. L'essentiel étant que pour tout kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp compris dans l'intervalle [0 ; 1], la nouvelle variable soit elle aussi comprise dans l'intervalle [0 ; 1].

Les interpolations les plus courantes se basant sur un changement de variable de l'interpolation linéaire sont les suivantes :

• Smoothstep : kitxmlcodeinlinelatexdvpu=3t^2-2t^3finkitxmlcodeinlinelatexdvp
• Smootherstep : kitxmlcodeinlinelatexdvpu=6t^5-15t^4+10t^3finkitxmlcodeinlinelatexdvp
• La parabole concave (accélération) : kitxmlcodeinlinelatexdvpu=t^2finkitxmlcodeinlinelatexdvp
• La parabole convexe (décélération) : kitxmlcodeinlinelatexdvpu=2t-t^2finkitxmlcodeinlinelatexdvp

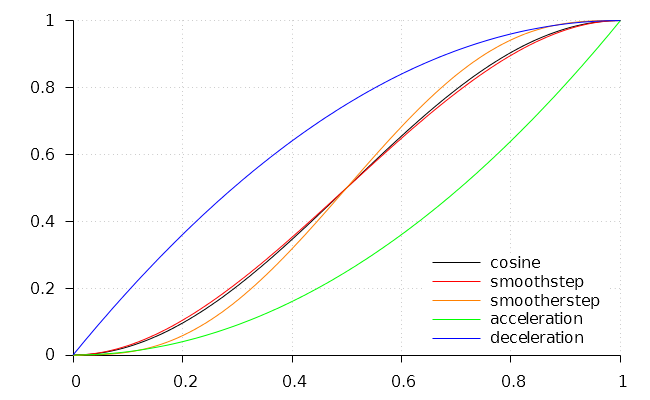
Sur la figure 6, on peut constater que la fonction smoothstep (courbe rouge) est très proche de la fonction cosinus (courbe noire) mais comme la fonction smoothstep est un polynôme cubique ne mettant en jeu que quelques additions et multiplications, ses performances seront meilleures. Ce type d'interpolation est d'ailleurs implémentée nativement dans les langages de shading pour le rendu d'images 3D.

La fonction smootherstep a été proposée par Ken Perlin (l'inventeur du bruit de Perlin) et a pour avantage d'avoir non seulement une dérivée première qui s'annule pour kitxmlcodeinlinelatexdvpt=0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpt=1finkitxmlcodeinlinelatexdvp comme pour smoothstep, mais également une dérivée seconde qui s'annule aussi en 0 et en 1 accentuant ainsi la courbure en 0 et en 1.

À la formule du changement de variable près, l'implémentation de ces quatre nouvelles formes d'interpolations est identique à celle de l'interpolation cosinusoïdale.

function smoothstep(y0: number, y1: number, t: number): number {
  var u = t*t*(3 - 2*t);
  return lerp(y0, y1, u);
}

function smootherstep(y0: number, y1: number, t: number): number {
  var u = t*t*t*(t*(t*6 - 15) + 10);
  return lerp(y0, y1, u);
}

function acceleration(y0: number, y1: number, t: number): number {
  var u = t*t;
  return lerp(y0, y1, u);
}

function deceleration(y0: number, y1: number, t: number): number {
  var u = t * (2 - t);
  return lerp(y0, y1, u);
}

Bien évidemment, il est possible d'imaginer bien d'autres changements de variable selon les besoins, néanmoins, les artefacts aux jonctions persisteront. Seules d'autres approches peuvent gommer ce qui peut être considéré comme un défaut.