Tout ce que nous avons vu jusqu'à présent consistait à relier des paires de points à l'aide de fonctions indépendantes pour obtenir au final une courbe plus ou moins « lisse ». C'est ce qu'on appelle l'interpolation par morceau.

Dans ce chapitre, nous montrerons qu'il existe une fonction interpolatrice capable de relier un nombre arbitraire de points en un seul tenant.

L'idée est de se dire qu'il doit peut-être exister un polynôme kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp dont la courbe représentative passe par tous les points initiaux.

Pour rappel, un polynôme est une fonction usuellement présentée sous la forme d'une somme de monômes kitxmlcodeinlinelatexdvpf(x)=a_0+a_1\,x+a_2\,x^2+\dots+a_{n-1}\,x^{n-1}+a_n\,x^nfinkitxmlcodeinlinelatexdvp tel que kitxmlcodeinlinelatexdvpa_0,a_1,\dots,a_nfinkitxmlcodeinlinelatexdvp sont les coefficients de ce polynôme et où la plus grande puissance de kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp correspond au degré de ce polynôme. À noter qu'ici les coefficients seront classés par ordre de puissance croissante par souci de cohérence avec les algorithmes.

Par exemple, une équation de droite (comme pour l'interpolation linéaire) kitxmlcodeinlinelatexdvpf(x)=a\,x+bfinkitxmlcodeinlinelatexdvp est un polynôme de degré 1 et de coefficients kitxmlcodeinlinelatexdvp(b,a)finkitxmlcodeinlinelatexdvp.

La fonction smoothstep kitxmlcodeinlinelatexdvpf(x)=3x^2-2x^3finkitxmlcodeinlinelatexdvp vue précédemment est un polynôme de degré 3 et de coefficients kitxmlcodeinlinelatexdvp(0,0,3,-2)finkitxmlcodeinlinelatexdvp.

Supposons que pour kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp points initiaux, il existe un polynôme kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp de degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp dont la courbe représentative passe par tous ces points. En se basant sur la forme usuelle d'un polynôme, cela revient à déterminer les kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp coefficients kitxmlcodeinlinelatexdvp(a_0, a_1, \dots, a_n)finkitxmlcodeinlinelatexdvp de ce polynôme à partir d'un système de Vandermonde :

Dans le cas général, un tel système est mal conditionné, c'est-à-dire, que les erreurs d'arrondi deviennent rapidement importantes et faussent significativement le calcul.

Pour remédier à cet écueil, on préférera utiliser une autre formulation des polynômes.

Pour contourner le système de Vandermonde, l'idée est de réécrire le polynôme kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp de degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp comme une combinaison linéaire de polynômes kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp de degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp possédant les propriétés suivantes :

1. Les polynômes kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp forment une base dans l'espace vectoriel des polynômes de degré inférieur ou égal à kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp.
2. kitxmlcodeinlinelatexdvpL_i(x_j) = \left\{\begin{matrix} 1 & \text{si}\;\; i= j,\\ 0 & \text{si}\;\; i\neq j. \end{matrix}\right.finkitxmlcodeinlinelatexdvp

Ces polynômes kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp sont communément nommés les polynômes d'interpolation de Lagrange.

La propriété 2 doit s'interpréter comme le fait que chaque polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp a pour racines les points initiaux kitxmlcodeinlinelatexdvpx_jfinkitxmlcodeinlinelatexdvp lorsque kitxmlcodeinlinelatexdvpj\neq ifinkitxmlcodeinlinelatexdvp (le polynôme s'annule). Lorsque kitxmlcodeinlinelatexdvpj=ifinkitxmlcodeinlinelatexdvp, le polynôme ne s'annule pas et voit sa valeur normalisée à 1.

Chaque polynôme kitxmlcodeinlinelatexdvpL_i(x_j)finkitxmlcodeinlinelatexdvp de degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp doit donc avoir kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp racines parmi les kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp points kitxmlcodeinlinelatexdvp\left\{x_0,\dots,x_n\right\}finkitxmlcodeinlinelatexdvp.

Ces polynômes peuvent donc s'écrire sous la forme d'un produit à kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp termes faisant apparaître les racines. Par exemple pour kitxmlcodeinlinelatexdvpi=0finkitxmlcodeinlinelatexdvp, un tel produit peut s'écrire kitxmlcodeinlinelatexdvp(x-x_1)(x-x_2)\dots(x-x_n)finkitxmlcodeinlinelatexdvp, pour kitxmlcodeinlinelatexdvpi=1finkitxmlcodeinlinelatexdvp, le produit s'écrit kitxmlcodeinlinelatexdvp(x-x_0)(x-x_2)\dots(x-x_n)finkitxmlcodeinlinelatexdvp, et ainsi de suite.

Plus généralement, pour un kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp donné, ce produit peut s'écrire ainsi :

Ce produit s'annule lorsqu'un de ses termes vaut zéro et donc lorsque pour un kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp donné, kitxmlcodeinlinelatexdvpx=x_jfinkitxmlcodeinlinelatexdvp tel que kitxmlcodeinlinelatexdvpj\neq ifinkitxmlcodeinlinelatexdvp. Par exemple, pour kitxmlcodeinlinelatexdvpi=0finkitxmlcodeinlinelatexdvp, si kitxmlcodeinlinelatexdvpx=x_2finkitxmlcodeinlinelatexdvp le produit s'annule puisque le facteur kitxmlcodeinlinelatexdvp(x_2-x_2)=0finkitxmlcodeinlinelatexdvp.

Par contre, pour un kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp donné, lorsque kitxmlcodeinlinelatexdvpx=x_ifinkitxmlcodeinlinelatexdvp, le produit ne s'annule pas. Autrement dit, pour chaque indice kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, il existe un point initial parmi les kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp points kitxmlcodeinlinelatexdvp\left\{x_0,\dots,x_n\right\}finkitxmlcodeinlinelatexdvp pour lequel le produit ne s'annule pas. Par exemple, pour kitxmlcodeinlinelatexdvpi=0finkitxmlcodeinlinelatexdvp, si kitxmlcodeinlinelatexdvpx=x_0finkitxmlcodeinlinelatexdvp le produit ne s'annule pas et ce produit vaut kitxmlcodeinlinelatexdvp(x_0-x_1)(x_0-x_2)\dots(x_0-x_n)finkitxmlcodeinlinelatexdvp.

Or, puisque nous souhaitons avoir une base normalisée et obtenir 1 pour kitxmlcodeinlinelatexdvpx=x_ifinkitxmlcodeinlinelatexdvp pour un kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp donné, il est nécessaire de diviser l'expression du produit par la valeur de ce produit quand kitxmlcodeinlinelatexdvpx=x_ifinkitxmlcodeinlinelatexdvp.

Les polynômes kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp ont donc la forme suivante :

Ceci peut également s'écrire de façon plus compacte avec la notation du produit indexé :

Il ne reste plus qu'à faire passer chaque polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp par l'ordonnée du point initial correspondant et à en faire la somme pour obtenir finalement le polynôme interpolateur kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp de degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp :

Ce polynôme vérifie par construction kitxmlcodeinlinelatexdvpf(x_i)=y_ifinkitxmlcodeinlinelatexdvp.

L'interpolation de Lagrange démontre donc l'existence d'un polynôme de degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp passant par kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp points, assertion uniquement présupposée à la section précédente.

Il est possible de transcrire littéralement en langage informatique l'expression du polynôme interpolateur de Lagrange à l'aide de deux boucles imbriquées.

function lagrange(X: number[], Y: number[], x: number): number {
  var sum = 0;
  for (var i = 0; i < X.length; i++) {
    var product = 1;
    for (var k = 0; k < X.length; k++) {
      if (k != i) {
        product *= (x - X[k]) / (X[i] - X[k]);
      }
    } // for k
    sum += Y[i] * product;
  } // for i
  return sum;
}

Le paramètre X est la liste des abscisses des points initiaux. Le paramètre Y est la liste des ordonnées des points initiaux tel que Y[0] correspond à l'ordonnée en X[0], Y[1] est la valeur en X[1] et ainsi de suite jusqu'à Y[n] où kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp est le nombre de valeurs initiales. Le paramètre x est l'abscisse du point à interpoler sur l'intervalle [X[0] ; X[n]]. La fonction retourne la valeur de l'interpolation de Lagrange en x.

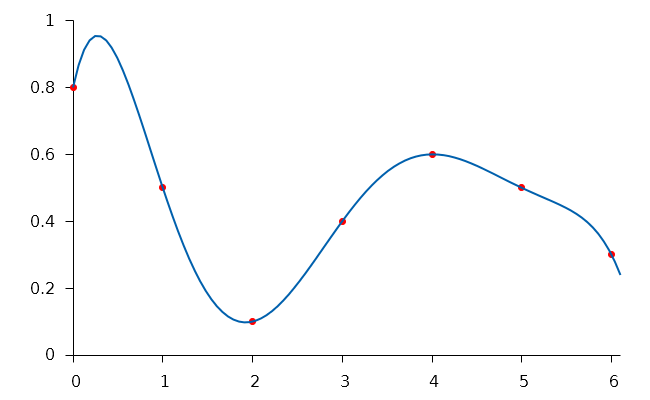
var y = lagrange([0, 1, 2, 3, 4, 5, 6], [0.8, 0.5, 0.1, 0.4, 0.6, 0.5, 0.3], 2.4);
// y === 0.17979647999999995

On peut noter que la complexité de cet algorithme est élevé. Il y a kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp additions et kitxmlcodeinlinelatexdvp(n-1)^2finkitxmlcodeinlinelatexdvp multiplications ce qui peut se révéler très coûteux en temps de calcul à mesure que le degré kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp et donc que le nombre de points à interpoler augmente. Même s'il est possible de faire appel à des algorithmes plus efficaces comme celui de Neville pour des petits degrés, il est souvent préférable de déterminer au préalable les coefficients du polynôme kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp et ensuite obtenir l'interpolation en kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp.

Pour calculer les coefficients de kitxmlcodeinlinelatexdvpf(x)=\sum_{i=0}^{n}y_i \, L_i(x)finkitxmlcodeinlinelatexdvp, une possibilité est de calculer les coefficients de chaque polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp, de les multiplier par kitxmlcodeinlinelatexdvpy_ifinkitxmlcodeinlinelatexdvp et ensuite de faire la somme pour chaque puissance de kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp.

Plus formellement, chaque polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp peut s'écrire sous la forme usuelle :

Par conséquent, chaque coefficient kitxmlcodeinlinelatexdvpa_kfinkitxmlcodeinlinelatexdvp du polynôme kitxmlcodeinlinelatexdvpf(x)=a_0\,x^n+a_1\,x^{n-1}+\dots+a_{n-2}\,x^2+a_{n-1}\,x+a_nfinkitxmlcodeinlinelatexdvp peut s'exprimer ainsi :

Pour calculer les coefficients kitxmlcodeinlinelatexdvp\alpha_{k,i}finkitxmlcodeinlinelatexdvp d'un polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp, posons :

À une racine près, ce nouveau polynôme kitxmlcodeinlinelatexdvp\gamma(x)finkitxmlcodeinlinelatexdvp a les même racines que celles de chaque polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp, de telle sorte qu'il est possible d'exprimer kitxmlcodeinlinelatexdvp\gamma(x)finkitxmlcodeinlinelatexdvp en fonction de kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp :

Cette relation permet de déduire les coefficients de kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp en fonction des coefficients de kitxmlcodeinlinelatexdvp\gamma(x)finkitxmlcodeinlinelatexdvp. qui eux peuvent s'obtenir par un simple développement successif des termes du produit.

Pour obtenir les coefficients de kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp, il suffit pour chacune des puissances de kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp, de sommer les coefficients des polynômes kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp correspondants multipliés par un facteur kitxmlcodeinlinelatexdvp\lambda_i=\frac{y_i}{\prod_{j \neq i}(x_i-x_j)}finkitxmlcodeinlinelatexdvp.

Armé de toutes ces relations, nous pouvons donc écrire un algorithme permettant de calculer les coefficients du polynôme interpolateur de Lagrange kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp.

function lagrangeCoefficients(X: number[], Y: number[]): number[] {
  var n = X.length - 1; // degrée
  // coeffs[] sont les coefficients du polynôme interpolateur f(x)
  var coeffs = new Array(n + 1);
  // beta[] sont les coefficients des polynômes L[i](x) (x-X[0])...(x-X[i-1])(x-X[i+1])...(x-X[n])
  var beta = Array(n + 1);

  // initialisation des coefficients
  for (var i = 0; i < n + 1; i++) {
    coeffs[i] = 0.0;
  } // for i

  // gamma[] sont les coefficients de (x-X[0])(x-X[1])...(x-X[n])
  var gamma = new Array(n + 2);
  gamma[0] = 1.0;
  for (var i = 0; i < n + 1; i++) {
    for (var j = i; j > 0; j--) {
      gamma[j] = gamma[j-1] - gamma[j] * X[i];
    } // for j
    gamma[0] *= -X[i];
    gamma[i+1] = 1;
  } // for i

  // calculs des coefficients
  for (var i = 0; i < n + 1; i++) {
    // dénominateur du polynôme d'interpolation de Lagrange Li(x)
    // denom = (X[i]-X[0])...(X[i]-X[i-1])(X[i]-X[i+1])...(X[i]-X[n])
    var denom = 1;
    for (var j = 0; j < n + 1; j++) {
      if (i != j) {
        denom *= X[i] - X[j];
      }
    } // for j

    var lambda = Y[i] / denom;
    beta[n] = gamma[n + 1]; // gamma[n1] = 1
    coeffs[n] += lambda * beta[n];
    for (var j = n - 1; j >= 0; j--) {
      beta[j] = gamma[j+1] + beta[j+1] * X[i];
      coeffs[j] += lambda * beta[j];
    } // for j
  } // for i

  return coeffs;
}

Le paramètre X est la liste des abscisses des points initiaux. Le paramètre Y est la liste des ordonnées des points initiaux tel que Y[0] correspond à l'ordonnée en X[0], Y[1] est la valeur en X[1] et ainsi de suite jusqu'à Y[n] où kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp est le nombre de valeurs initiales. La fonction lagrangeCoefficients() retourne la liste des coefficients du polynôme interpolateur de Lagrange kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp par ordre de puissance croissante.

var fCoeffs = lagrangeCoefficients([0, 1, 2, 3, 4, 5, 6], [0.8, 0.5, 0.1, 0.4, 0.6, 0.5, 0.3]);
// fCoeffs === [
//   0.8,
//   1.256666666666667,
//   -3.013333333333334,
//   1.9250000000000007,
//   -0.5333333333333337,
//   0.06833333333333334,
//   -0.003333333333333334]

Une fois que nous avons les coefficients d'un polynôme, il est relativement simple et efficace de calculer sa valeur en un point à l'aide par exemple de la méthode de Horner.

function horner(A: number[], x: number): number {
  var n = A.length - 1; // degré
  var result = 0;

  for (var i = n; i >= 0; i--) {
    result = result * x + A[i];
  } // for i

  return result;
}

Le paramètre A représente la liste des coefficients par degré croissant du polynôme à évaluer. Le paramètre x est l'abscisse du point à évaluer par le polynôme. La fonction horner() renvoie donc la valeur en x du polynôme de coefficients A.

Connaissant les coefficients, la complexité est en kitxmlcodeinlinelatexdvpO(n)finkitxmlcodeinlinelatexdvp. Ainsi, il est donc possible de calculer efficacement un grand nombre de valeurs d'interpolation.

Cependant, bien qu'il soit plus efficace dans l'absolu de pré-calculer les coefficients du polynôme interpolateur que d'utiliser naïvement la formule de Lagrange en chaque point à interpoler, une rapide évaluation de la complexité de la fonction lagrangeCoefficients() indique tout de même une complexité en kitxmlcodeinlinelatexdvpO(n^2)finkitxmlcodeinlinelatexdvp. Autrement dit, à partir d'un certain nombre de points, l'interpolation de Lagrange devient coûteuse.

D'autant plus qu'ajouter un nouveau point nous oblige recalculer chaque polynôme kitxmlcodeinlinelatexdvpL_i(x)finkitxmlcodeinlinelatexdvp et chaque coefficient sans pouvoir réutiliser des résultats antérieurs à l'ajout de ce nouveau point.

Enfin, bien que préférable à la résolution d'un système de Vandermonde, cette méthode reste sensible aux erreurs d'arrondi.

L'interpolation de Newton respecte les même conditions que l'interpolation de Lagrange, à savoir kitxmlcodeinlinelatexdvpf(x_i)=y_ifinkitxmlcodeinlinelatexdvp où pour tout point initial kitxmlcodeinlinelatexdvp(x_i,y_i)finkitxmlcodeinlinelatexdvp. Le polynôme sous-jacent est le même que celui obtenu par la forme de Lagrange. C'est pourquoi il est plus correct de parler de forme de Newton car seule la formulation diffère. La forme de Newton est donc en quelque sorte un autre algorithme pour déterminer le polynôme interpolateur avec pour but avoué de calculer plus efficacement les valeurs du polynôme interpolateur.

Nous avons vu avec l'interpolation de Lagrange qu'il était possible d'exprimer le polynôme interpolateur kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp à partir d'une certaine base de polynômes. Avec la forme de Newton, l'idée est de se donner une autre base de telle sorte que l'ajout d'un nouveau point initial ne nous obligera pas de recalculer les polynômes de cette base, mais simplement d'adjoindre un nouveau polynôme à la base déjà existante.

Pour cela, commençons par ne considérer que le premier point initial kitxmlcodeinlinelatexdvp(x_0,y_0)finkitxmlcodeinlinelatexdvp.

Cherchons un polynôme kitxmlcodeinlinelatexdvpf_0(x)finkitxmlcodeinlinelatexdvp de degré 0 tel que kitxmlcodeinlinelatexdvpf_0(x_0)=y_0finkitxmlcodeinlinelatexdvp.

C'est très simple. C'est le polynôme constant de coefficient kitxmlcodeinlinelatexdvp\alpha_0=y_0finkitxmlcodeinlinelatexdvp. On a donc kitxmlcodeinlinelatexdvpf_0(x)=\alpha_0finkitxmlcodeinlinelatexdvp.

Ajoutons ensuite un nouveau point kitxmlcodeinlinelatexdvp(x_1, y_1)finkitxmlcodeinlinelatexdvp.

Cherchons un polynôme kitxmlcodeinlinelatexdvpf_1(x)finkitxmlcodeinlinelatexdvp de degré 1 vérifiant les conditions d'interpolation kitxmlcodeinlinelatexdvpf_1(x_0)=y_0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf_1(x_1)=y_1finkitxmlcodeinlinelatexdvp et s'exprimant en fonction de kitxmlcodeinlinelatexdvpf_0(x)finkitxmlcodeinlinelatexdvp.

Ce polynôme peut s'écrire ainsi : kitxmlcodeinlinelatexdvpf_1(x)=f_0(x)+\alpha_1 (x-x_0)finkitxmlcodeinlinelatexdvp.

Comme kitxmlcodeinlinelatexdvpf_1(x_0)=y_0+\alpha_1(x_0-x_0)=y_0finkitxmlcodeinlinelatexdvp, avec kitxmlcodeinlinelatexdvp\alpha_1finkitxmlcodeinlinelatexdvp coefficient réel, la première condition d'interpolation est donc vérifiée.

Déterminons le coefficient kitxmlcodeinlinelatexdvp\alpha_1finkitxmlcodeinlinelatexdvp de façon à vérifier la seconde condition d'interpolation :

Typiquement, kitxmlcodeinlinelatexdvp\alpha_1finkitxmlcodeinlinelatexdvp est la pente de la droite d'équation kitxmlcodeinlinelatexdvpf_1(x)finkitxmlcodeinlinelatexdvp (et kitxmlcodeinlinelatexdvp\alpha_0finkitxmlcodeinlinelatexdvp l'ordonnée à l'origine).

Ajoutons ensuite un nouveau point kitxmlcodeinlinelatexdvp(x_2,y_2)finkitxmlcodeinlinelatexdvp et cherchons un polynôme kitxmlcodeinlinelatexdvpf_2(x)finkitxmlcodeinlinelatexdvp en poursuivant le processus.

On a bien par construction kitxmlcodeinlinelatexdvpf_2(x_0)=y_0,f_2(x_1)=y_1finkitxmlcodeinlinelatexdvp. Reste à déterminer le coefficient kitxmlcodeinlinelatexdvp\alpha_2finkitxmlcodeinlinelatexdvp pour que kitxmlcodeinlinelatexdvpf_2(x_2)=y_2finkitxmlcodeinlinelatexdvp.

Après un rapide calcul on obtient :

En généralisant, ajoutons un kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvpème point kitxmlcodeinlinelatexdvp(x_i,y_i)finkitxmlcodeinlinelatexdvp à un ensemble de kitxmlcodeinlinelatexdvpi-1finkitxmlcodeinlinelatexdvp points déjà existants.

Pour un ensemble de kitxmlcodeinlinelatexdvpi-1finkitxmlcodeinlinelatexdvp points et son polynôme interpolateur kitxmlcodeinlinelatexdvpf_{i-1}(x)finkitxmlcodeinlinelatexdvp, il est donc possible d'ajouter un nouveau point et d'exprimer le nouveau polynôme interpolateur kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp en fonction kitxmlcodeinlinelatexdvpf_{i-1}(x)finkitxmlcodeinlinelatexdvp. Les produits des termes faisant apparaître les racines kitxmlcodeinlinelatexdvpN_i(x)=(x-x_0)(x-x_1)\dots(x-x_{i-1})finkitxmlcodeinlinelatexdvp sont appelés polynômes de Newton et forment une base.

Le polynôme interpolateur kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp peut ainsi s'écrire comme une combinaison linéaire de ces polynômes de Newton :

Il ne reste à présent qu'à expliciter les coefficients kitxmlcodeinlinelatexdvp\alpha_ifinkitxmlcodeinlinelatexdvp que nous nommerons coefficients de Newton. Ils peuvent s'exprimer sous la forme de différences divisées, usuellement notées […], tel que kitxmlcodeinlinelatexdvp\alpha_i=[y_0,\dots,y_i]finkitxmlcodeinlinelatexdvp.

Les différences divisées sont une succession de divisions définies de manière récursive :

D'où kitxmlcodeinlinelatexdvpf(x)=\sum_{i=0}^{n}\left [y_0,\dots,y_i\right ] N_i(x)finkitxmlcodeinlinelatexdvp.

Pour implémenter l'interpolation de Newton, nous avons donc besoin d'une fonction calculant tout d'abord les différences divisées puis d'une autre calculant la valeur interpolée proprement dite via la formule de kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp et des polynômes kitxmlcodeinlinelatexdvpN_i(x)finkitxmlcodeinlinelatexdvp.

function divDiffsRec(X: number[], Y: number[]): number {
    if (X.length === 1) {
        return Y[0];
    }
    else {
        return (
            divDiffsRec(X.slice(1, X.length), Y.slice(1, Y.length)) -
            divDiffsRec(X.slice(0, X.length - 1), Y.slice(0, Y.length - 1))
        ) / (X[X.length - 1] - X[0]);
    }
}

Le paramètre X est la liste des abscisses des points initiaux. Le paramètre Y est la liste des ordonnées des points initiaux tel que Y[0] correspond à l'ordonnée en X[0], Y[1] est la valeur en X[1] et ainsi de suite jusqu'à Y[n]. La fonction divDiffsRec() renvoie la valeur des différences divisées selon les vecteurs X et Y.

var alphaN = divDiffsRec([0, 1, 2, 3, 4, 5, 6], [0.8, 0.5, 0.1, 0.4, 0.6, 0.5, 0.3]);
// alphaN === -0.0033333333333333353

Nous pouvons donc définir une fonction permettant de calculer l'interpolation en un point donné à l'aide des différences divisées.

function newtonRec(X: number[], Y: number[], x: number): number {
    var sum = 0;
    for (var i = 0; i < Y.length; i++) {
        var product = 1;
        for (var k = 0; k < i; k++) {
            if (k != i) {
                product *= x - k;
            }
        } // for k
        sum += divDiffsRec(X.slice(0, i+1), Y.slice(0, i+1)) * product;
    } // for i
    return sum;
}

La fonction newton() appelée avec les même paramètres que ceux utilisés plus haut pour la fonction lagrange() renvoie sans surprise le même résultat.

var y = newton([0, 1, 2, 3, 4, 5, 6], [0.8, 0.5, 0.1, 0.4, 0.6, 0.5, 0.3], 2.4);
// y === 0.17979647999999995

Cette implémentation de l'interpolation de Newton utilisant les différences divisées récursives, bien qu'absolument correcte, a un défaut qui est de réaliser des calculs redondants sur les différences divisées intermédiaires. En effet dans la boucle principale, à l'itération kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvp\left [y_0,\dots,y_i\right ]finkitxmlcodeinlinelatexdvp dépend de kitxmlcodeinlinelatexdvp\left [y_0,\dots,y_{i-1}\right ]finkitxmlcodeinlinelatexdvp qui a été calculé à l'itération kitxmlcodeinlinelatexdvpi-1finkitxmlcodeinlinelatexdvp.

Pour optimiser, nous pourrions simplement mémoriser les différences divisées de l'itération précédente. Cependant, il est possible de faire mieux en reconsidérant le calcul des différences divisées non plus de façon récursive, transcription directe de sa définition, mais de façon itérative, en construisant au fur et à mesure une liste kitxmlcodeinlinelatexdvp(\alpha_0,\alpha_1,\dots,\alpha_n)finkitxmlcodeinlinelatexdvp des coefficients de Newton.

Ces derniers pourront ainsi être utilisés efficacement soit par l'implémentation précédente de l'interpolation de Newton, soit par un algorithme de type méthode de Horner comme vue précédemment qui s'applique aisément à la forme de Newton.

function divDiffsIter(X: number[], Y: number[]): number[] {
  var n = X.length - 1; // degré
  var alphas = Y; // initialisation des différences divisées

  for (var i = 0; i < n; i++) {
    for (var j = n; j > i; j--) {
      alphas[j] = (alphas[j] - alphas[j - 1]) / (X[j] - X[j - i - 1]);
    } // for j
  } // for i

  return alphas;
}

Le paramètre X est la liste des abscisses des points initiaux. Le paramètre Y est la liste des ordonnées des points initiaux tel que Y[0] correspond à l'ordonnée en X[0], Y[1] est la valeur en X[1] et ainsi de suite jusqu'à Y[n].

var alphas = divDiffsIter([0, 1, 2, 3, 4, 5, 6], [0.8, 0.5, 0.1, 0.4, 0.6, 0.5, 0.3]);
// alphas === [
//   0.8,
//   -0.30000000000000004,
//   -0.04999999999999999,
//   0.13333333333333333,
//   -0.06666666666666668,
//   0.01833333333333334,
//   -0.0033333333333333353]

À l'aide de cette nouvelle implémentation des différences divisées et en utilisant la méthode de Horner, nous pouvons réécrire l'interpolation de Newton pour un point donné.

function newtonHorner(X: number[], alphas: number[], x: number): number {
  var n = X.length - 1; // degré
  var result = 0;

  for (var i = n; i >= 0; i--) {
    result = result * (x - X[i]) + alphas[i];
  } // for i

  return result;
}

Le paramètre X est la liste des abscisses des points initiaux. Le paramètre alphas correspond aux coefficients de Newton calculés préalablement, par exemple à l'aide des différences divisées. Le paramètre x est l'abscisse du point à interpoler sur l'intervalle [X[0] ; X[n]]. La fonction newtonHorner() renvoie la valeur de l'interpolation en x.

var alphas = divDiffsIter([0, 1, 2, 3, 4, 5, 6], [0.8, 0.5, 0.1, 0.4, 0.6, 0.5, 0.3]);
var y = newtonHorner([0, 1, 2, 3, 4, 5, 6], alphas, 2.4);
// y === 0.17979648000000004

C'est cette méthode qui est la plus couramment utilisée pour l'interpolation polynômiale.

Bien que nous n'ayons pas réellement besoin de calculer les coefficients kitxmlcodeinlinelatexdvpa_ifinkitxmlcodeinlinelatexdvp du polynôme de kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp, cela reste tout à fait possible via les coefficients de Newton kitxmlcodeinlinelatexdvp\alpha_ifinkitxmlcodeinlinelatexdvp. Cela est tout de même coûteux puisque la complexité de l'algorithme correspondant reste en kitxmlcodeinlinelatexdvpO(n^2)finkitxmlcodeinlinelatexdvp comme son homologue pour la méthode de Lagrange.

function lagrangeCoefficientsNewton(X: number[], alphas: number[]): number[] {
  var n = X.length - 1; // degré
  // coeffs[] sont les coefficients du polynôme interpolateur f(x)
  var coeffs = new Array(n + 1);

  // initialisation des coefficients
  for (var i = 0; i < n + 1; i++) {
    coeffs[i] = 0.0;
  } // for i

  coeffs[0] = alphas[n];
  for (var i = n - 1; i >= 0; i--) {
    for (var j = n - i; j > 0; j--) {
      coeffs[j] = coeffs[j-1] - X[i] * coeffs[j];
    } // for j
    coeffs[0] = alphas[i] - X[i] * coeffs[0];
  } // for i

  return coeffs;
}

Qu'elle utilise la méthode de Lagrange ou de Newton, l'interpolation polynomiale produit une courbe représentative plus régulière, plus lisse, que les interpolations par morceaux vues précédemment. Néanmoins, malgré les méthodes et algorithmes pour calculer efficacement les valeurs, elle nécessite de manipuler des polynômes de degré potentiellement élevé, directement fonction du nombre de points initiaux. De plus, dans le cas particulier mais pourtant fréquent où les points sont équirépartis comme c'est l'hypothèse dans cet article, les valeurs tendent à osciller à mesure que le degré du polynôme augmente. C'est le phénomène de Runge qui rend les valeurs de moins en moins cohérentes. Ce qui est un peu paradoxal.

Par conséquence, dans les situations où le nombre de points initiaux est élevé, par exemple 100, 1 000, 10 000 voire davantage, une interpolation polynomiale de Lagrange ou de Newton est à exclure.