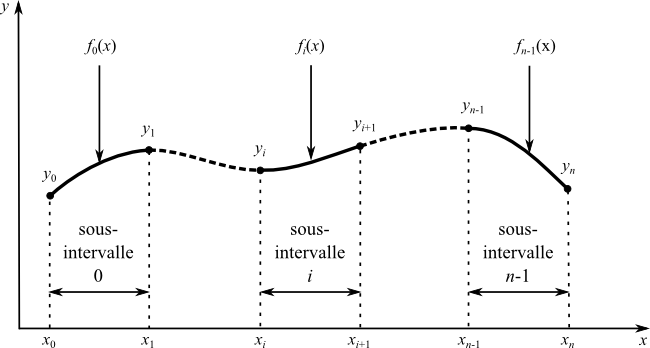
8. Splines▲
8-1. Principes▲
Les techniques que nous avons rencontrées jusqu'à présent comportent certes des qualités, mais également des inconvénients majeurs.
Les fonctions simples par morceaux présentent des irrégularités aux jonctions, elles ne sont pas dérivables sur l'ensemble de l'intervalle [kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp]. Cela est dû à leur caractère local.
L'interpolation polynomiale de Lagrange (ou de Newton), bien que dérivable sur [kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp], a quant à elle une complexité croissante à mesure que le nombre de points à interpoler augmente. Cela est dû à son caractère global.
L'idéal serait de conjuguer la simplicité et la flexibilité de l'interpolation par morceaux, avec la régularité et la dérivabilité de l'interpolation polynomiale.
Pour cela, il existe une technique au caractère intermédiaire entre le niveau local d'une interpolation simple par morceau et le niveau global d'une interpolation polynomiale de Lagrange. Il s'agit du concept de spline, fonction polynomiale par morceaux, qui se veut « lisse » sur l'ensemble de l'intervalle, et en particulier aux points de jonction qu'on appelle aussi des nœuds.
Les splines sont basées sur l'interpolation de Hermite. De façon schématique, ce type d'interpolation étend non seulement les conditions sur les valeurs aux nœuds de la fonction d'interpolation comme vu au chapitre précédent, mais aussi sur ses dérivées.
C'est pourquoi l'interpolation par splines peut être considérée comme une technique semi-locale ou semi-globale, c'est selon.
Plus formellement, une spline est une fonction kitxmlcodeinlinelatexdvpf(x)finkitxmlcodeinlinelatexdvp définie par morceaux sur un intervalle [kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp]. Au kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvpème sous-intervalle [kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_{i+1}finkitxmlcodeinlinelatexdvp] est défini un morceau de la spline que nous noterons kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp.
Chaque fonction kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp est un polynôme devant vérifier les conditions d'interpolations kitxmlcodeinlinelatexdvpf_i(x_i)=y_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf_i(x_{i+1})=y_{i+1}finkitxmlcodeinlinelatexdvp.
Pour assurer continuité et la dérivabilité sur l'ensemble de l'intervalle (et notamment aux jonctions), une spline impose également les conditions suivantes :
kitxmlcodelatexdvp\begin{align} f_i(x_{i+1})&=f_{i+1}(x_{i+1}) &\small\text{(continuité de la spline)}\\ f'_i(x_{i+1})&=f'_{i+1}(x_{i+1}) &\small\text{(continuité de la dérivée première)}\\ f''_i(x_{i+1})&=f''_{i+1}(x_{i+1}) &\small\text{(continuité de la dérivée seconde)}\\ \dots\\ f^{(k)}_i(x_{i+1})&=f^{(k)}_{i+1}(x_{i+1}) &\small\text{(continuité de la dérivée d'ordre }\textit{k}\text{)} \end{align}finkitxmlcodelatexdvpPour assurer la dérivabilité d'ordre 1, il est nécessaire que le polynôme kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp soit de degré supérieur ou égal à deux. En généralisant, on montre que pour assurer une dérivabilité jusqu'à un ordre kitxmlcodeinlinelatexdvpkfinkitxmlcodeinlinelatexdvp, il est nécessaire que kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp soit un polynôme de degré supérieur ou égal à kitxmlcodeinlinelatexdvpk+1finkitxmlcodeinlinelatexdvp.
Plus le degré des morceaux kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp sera élevé, plus la spline aura un aspect lisse, mais en contrepartie, plus les calculs seront coûteux. C'est pourquoi en pratique on se limite à des splines cubiques constituées de polynômes de degré 3.
Il est donc possible d'imposer à de telles splines des conditions de dérivabilité aux nœuds jusqu'à l'ordre 2. Au-delà, les dérivées s'annulent.
8-2. Spline de Hermite▲
Les splines de Hermite sont une famille de splines cubiques se limitant à être une fois continûment dérivable (classe kitxmlcodeinlinelatexdvpC^1finkitxmlcodeinlinelatexdvp) sur l'intervalle [kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp].
Cela rend cette famille de splines plus simple à manipuler par rapport au cas général d'une continuité en kitxmlcodeinlinelatexdvpC^2finkitxmlcodeinlinelatexdvp.
Posons le changement de variable kitxmlcodeinlinelatexdvpt=\frac{x-x_i}{x_{i+1}-x_i}finkitxmlcodeinlinelatexdvp. On peut obtenir ainsi une fonction kitxmlcodeinlinelatexdvps_i(t)finkitxmlcodeinlinelatexdvp dans l'intervalle [0 ; 1] équivalente à la fonction kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp dans le kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvpème sous-intervalle [kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_{i+1}finkitxmlcodeinlinelatexdvp].
L'expression générale d'un morceau de spline, qui est ici un polynôme de degré 3, et de sa dérivée première peut donc s'écrire :
kitxmlcodelatexdvp\begin{align} s_i(t)&=a_{i,0}+a_{i,1}\cdot t_i+a_{i,2}\cdot t_i^2+a_{i,3}\cdot t_i^3\\ s_i'(t)&=a_{i,1}+2\,a_{i,2}\cdot t_i+3\,a_{i,3}\cdot t_i^2n \end{align}finkitxmlcodelatexdvpEn kitxmlcodeinlinelatexdvpt=0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpt=1finkitxmlcodeinlinelatexdvp, on obtient les valeurs de kitxmlcodeinlinelatexdvps_i(t)finkitxmlcodeinlinelatexdvp et de sa dérivée :
kitxmlcodelatexdvp\begin{align} s_i(0)&=a_{i,0}\\ s_i(1)&=a_{i,0}+a_{i,1}+a_{i,2}+a_{i,3}\\ s_i'(0)&=a_{i,1}\\ s_i'(1)&=a_{i,1}+2\,a_{i,2}+3\,a_{i,3} \end{align}finkitxmlcodelatexdvpCeci nous permet d'exprimer les quatre coefficients kitxmlcodeinlinelatexdvpa_{i,0}finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpa_{i,1}finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpa_{i,2}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpa_{i,3}finkitxmlcodeinlinelatexdvp de notre morceau de spline :
kitxmlcodelatexdvp\begin{cases} a_{i,0}=s_i(0)\\ a_{i,1}=s_i'(0)\\ a_{i,2}=-3\,s_i(0)+3\,s_i(1)-2\,s_i'(0)-s_i'(1)\\ a_{i,3}=2\,s_i(0)-2\,s_i(1)+s_i'(0)+s_i'(1) \end{cases}finkitxmlcodelatexdvpEn utilisant les conditions d'interpolation on obtient :
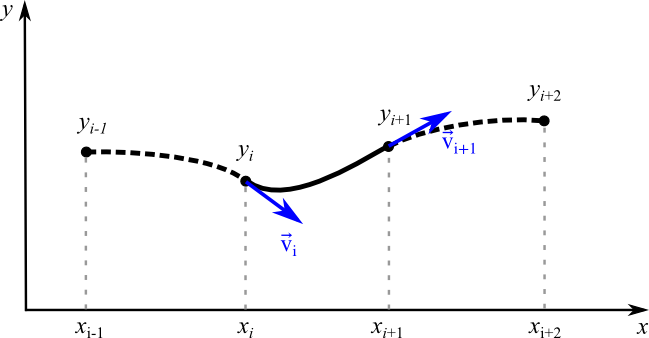
kitxmlcodelatexdvp\begin{cases} a_{i,0}=y_i\\ a_{i,1}=m_i\\ a_{i,2}=-3\,y_i+3\,y_{i+1}-2\,m_i-m_{i+1}\\ a_{i,3}=2\,y_i-2\,y_{i+1}+m_i+m_{i+1} \end{cases}finkitxmlcodelatexdvpavec kitxmlcodeinlinelatexdvpm_i=s_i'(0)finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpm_{i+1}=s_i'(1)finkitxmlcodeinlinelatexdvp les pentes des tangentes kitxmlcodeinlinelatexdvp\overrightarrow{v}_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\overrightarrow{v}_{i+1}finkitxmlcodeinlinelatexdvp (cf. figure 13) aux nœuds kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpi+1finkitxmlcodeinlinelatexdvp. Il est facile de deviner que ces pentes influencent l'aspect de la spline en chaque nœud.
Il est courant d'utiliser la représentation matricielle pour caractériser les polynômes d'une spline où chaque ligne de la matrice correspond au développement de chaque coefficient kitxmlcodeinlinelatexdvpa_{i,0}finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpa_{i,1}finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpa_{i,2}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpa_{i,3}finkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvps_i(t)=(1, t, t^2, t^3) \cdot \left (\begin{array}{rrrr} 1&0&0&0\\ 0&0&1&0\\ -3&3&-2&-1\\ 2&-2&1&1\\ \end{array} \right ) \cdot \left (\begin{array}{cccc} y_i\\ y_{i+1}\\ m_i\\ m_{i+1} \end{array}\right )finkitxmlcodelatexdvpLa matrice principale est appelée matrice de base. À partir de ses colonnes, il est possible d'extraire les fonctions de base de Hermite permettant de réécrire les polynômes de la spline :
kitxmlcodelatexdvps_i(t)=h_0(t)\cdot y_i+h_1(t)\cdot y_{i+1}+h_2(t)\cdot m_i+h_3(t)\,m_{i+1}finkitxmlcodelatexdvpavec
kitxmlcodelatexdvp\begin{cases} h_0(t)=1-3\,t^2+2\,t^3\\ h_1(t)=3\,t^2-2\,t^3\\ h_2(t)=t-2\,t^2+t^3\\ h_3(t)=-t^2+t^3 \end{cases}finkitxmlcodelatexdvpCette forme présente les polynômes indépendamment des valeurs et des pentes des tangentes aux nœuds. Elle est intéressante puisqu'elle permet d'optimiser les calculs de tracé de splines. Si on se donne un pas de tracé constant ce qui correspond à une subdivision fixe de l'intervalle [0 ; 1] de la variable kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp, les valeurs des fonctions de base de Hermite pour chacun des pas ne seront à calculer qu'une seule fois pour un sous-intervalle kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, et pourront ensuite être réutilisées pour tous les autres sous-intervalles. La valeur d'interpolation n'étant ensuite qu'une somme de quatre multiplications.
L'implémentation ci-dessous de l'interpolation par spline cubique de Hermite n'intègre pas cette optimisation. Il s'agit simplement d'une transcription directe des formules.
function hermiteSpline(y0: number, y1: number, m0: number, m1: number, t: number): number {
var t2 = t * t;
var t3 = t2 * t;
// Calcul des fonctions de base d'une spline de Hermite
var b0 = 1 - 3 * t2 + 2 * t3;
var b1 = 3 * t2 - 2 * t3;
var b2 = t - 2 * t2 + t3;
var b3 = - t2+ t3;
return b0 * y0 + b1 * y1 + b2 * m0 + b3 * m1;
}|
Implémentation de l'interpolation par spline cubique de Hermite |
Les paramètres y0 et y1 correspondent aux valeurs des nœuds en kitxmlcodeinlinelatexdvpt=0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpt=1finkitxmlcodeinlinelatexdvp. Les paramètres m0 et m1 correspondent aux pentes respectives. Et le paramètre t compris entre 0 et 1 correspond à la position relative sur l'axe l'abscisse entre les deux nœuds concernés. La fonction hermiteSpline() renvoie l'interpolation par spline cubique de Hermite en t.
Les pentes kitxmlcodeinlinelatexdvpm_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpm_{i+1}finkitxmlcodeinlinelatexdvp des deux tangentes peuvent ne pas être connues au préalable.
Il existe diverses façons de les définir en fonction du rendu final souhaité. Les principales sont la forme de Catmull-Rom et celle plus générale dite cardinale ou canonique.
8-3. Spline de Catmull-Rom▲
Dans l'hypothèse où les nœuds sont répartis de façon plus ou moins homogène, une spline cubique de Catmull-Rom définie chaque tangente à un nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp comme parallèle à la droite passant par les nœuds kitxmlcodeinlinelatexdvpi-1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpi+1finkitxmlcodeinlinelatexdvp. Autrement dit, la pente kitxmlcodeinlinelatexdvpm_ifinkitxmlcodeinlinelatexdvp de la tangente en chaque nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp s'exprime ainsi :
kitxmlcodelatexdvpm_i=\frac{y_{i+1}-y_{i-1}}{x_{i+1}-x_{i-1}}finkitxmlcodelatexdvpLes paramètres kitxmlcodeinlinelatexdvpm_ifinkitxmlcodeinlinelatexdvp étant déduits des nœuds, cela signifie que l'inclinaison locale de la spline suit la direction des nœuds avoisinants.
Dans la situation où les nœuds sont équirépartis, l'expression des pentes kitxmlcodeinlinelatexdvpm_ifinkitxmlcodeinlinelatexdvp se simplifie et donne :
kitxmlcodelatexdvpm_i=\frac{y_{i+1}-y_{i-1}}{2}finkitxmlcodelatexdvpCe qui permet d'obtenir la forme courante des polynômes d'une spline cubique de Catmull-Rom avec kitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp dans l'intervalle [0 ; 1] :
kitxmlcodelatexdvp\begin{align} s_i(t)&=y_i\\ &+(\frac{1}{2}\,y_{i-1}+\frac{1}{2}\,y_{i+1})\,t\\ &+(y_{i-1}-\frac{5}{2}\,y_i+2\,y_{i+1}-\frac{1}{2}\,y_{i+2})\,t^2\\ &+(-\frac{1}{2}\,y_{i-1}+\frac{3}{2}\,y_i-\frac{3}{2}\,y_{i+1}+\frac{1}{2}\,y_{i+2})\,t^3 \end{align}finkitxmlcodelatexdvpCes polynômes peuvent s'écrire sous leur forme matricielle :
kitxmlcodelatexdvps_i(t)=(1, t, t^2, t^3) \cdot \frac{1}{2} \left (\begin{array}{rrrr} 0&2&0&0\\ -1&0&1&0\\ 2&-5&4&-1\\ -1&3&-3&1 \end{array} \right ) \cdot \left (\begin{array}{cccc} y_{i-1}\\ y_i\\ y_{i+1}\\ y_{i+2} \end{array}\right )finkitxmlcodelatexdvpD'où l'implémentation suivante :
function catmullromSpline(y0: number, y1: number, y2: number, y3: number, t: number): number {
var t2 = t * t;
var t3 = t2 * t;
// Calcul des fonctions de base d'une spline de Catmull-Rom
var b0 = -t + 2 * t2 - t3;
var b1 = 2 - 5 * t2 + 3 * t3;
var b2 = t + 4 * t2 - 3 * t3;
var b3 = -t2 + t3;
return (b0 * y0) + (b1 * y1) + (b2 * y2) + (b3 * y3);
}|
Implémentation de l'interpolation par spline cubique de Catmull-Rom |
Les paramètres y0, y1, y2 et y3 correspondent respectivement aux valeurs des nœuds kitxmlcodeinlinelatexdvpi-1finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvpi+1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpi+2finkitxmlcodeinlinelatexdvp. Le paramètre t correspond à l'abscisse relative entre les nœuds correspondant à y1 et y2. La fonction catmullromSpline() renvoie l'interpolation selon la spline de Catmull-Rom.
Comme précédemment avec les splines de Hermite, la spline de Catmull-Rom n'étant qu'un cas particulier, il est possible d'optimiser en pré-calculant les différentes valeurs des fonctions de base sur l'intervalle [0 ; 1].
Même si nous avons à présent l'algorithme de la spline de Catmull-Rom, il nous reste encore à traiter le cas des bords.
Pour le premier sous-intervalle [kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_1finkitxmlcodeinlinelatexdvp] (resp. le dernier sous-intervalle [kitxmlcodeinlinelatexdvpx_{n-1}finkitxmlcodeinlinelatexdvp ; kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp]), la valeur de la pente kitxmlcodeinlinelatexdvpm_0finkitxmlcodeinlinelatexdvp (resp. kitxmlcodeinlinelatexdvpm_nfinkitxmlcodeinlinelatexdvp) ne peut pas se déduire de la formule de la pente car le nœud kitxmlcodeinlinelatexdvp-1finkitxmlcodeinlinelatexdvp (resp kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp) n'existe pas. Pour se doter de nœuds imaginaires complémentaires, plusieurs conventions possibles peuvent alors être adoptées dont les suivantes :
- L'une des plus simples d'entre elles consiste à se donner un nœud imaginaire ayant la même valeur que le nœud voisin. Ce qui revient à définir :
- Une autre convention consiste à placer un nœud imaginaire kitxmlcodeinlinelatexdvp-1finkitxmlcodeinlinelatexdvp (resp. kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp) sur la droite passant par les nœuds kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp (resp. kitxmlcodeinlinelatexdvpn-1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp), de telle sorte que le nœud kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp (resp. kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp) soit le milieu du segment ayant pour extrémités les nœuds kitxmlcodeinlinelatexdvp-1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp (resp. kitxmlcodeinlinelatexdvpn-1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp). Ce qui revient à définir :
8-4. Spline cardinale▲
Une spline cardinale, nommée également spline canonique, est une forme plus générale d'une spline de Catmull-Rom où est introduit un paramètre supplémentaire, la tension.
La pente kitxmlcodeinlinelatexdvpm_ifinkitxmlcodeinlinelatexdvp d'une tangente en plus de dépendre des points voisins, dépend ici d'une tension notée kitxmlcodeinlinelatexdvpwfinkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpm_i=(1-w)\frac{y_{i+1}-y_{i-1}}{x_{i+1}-x_{i-1}}finkitxmlcodelatexdvpDe façon imagée, la tension peut être assimilée à la longueur de la tangente. Plus la tension d'une tangente est élevée, et plus cette tangente se rapprochera de la perpendiculaire à la droite parallèle passant par les deux nœuds immédiatement voisins.
On constate aussi qu'une spline de Catmull-Rom n'est qu'une spline cardinale particulière où la tension kitxmlcodeinlinelatexdvpwfinkitxmlcodeinlinelatexdvp est nulle.
En se plaçant dans le cas de nœuds équirépartis et en posant kitxmlcodeinlinelatexdvpu=\frac{1-w}{2}finkitxmlcodeinlinelatexdvp, on a :
kitxmlcodelatexdvpm_i=u\,(y_{i+1}-y_{i-1})finkitxmlcodelatexdvpCe qui nous permet de déduire la matrice de base d'une spline cardinale à partir d'une spline de Hermite (cf. § 8.2) :
kitxmlcodelatexdvps_i(t)=(1, t, t^2, t^3) \cdot \left (\begin{array}{cccc} 0&1&0&0\\ -u&0&u&0\\ 2u&u-3&3-2u&-u\\ -u&2-u&u-2&u \end{array} \right ) \cdot \left (\begin{array}{cccc} y_{i-1}\\ y_i\\ y_{i+1}\\ y_{i+2} \end{array}\right )finkitxmlcodelatexdvpOn déduit aisément de la matrice de base l'implémentation suivante en TypeScript.
function cardinalSpline(y0: number, y1: number, y2: number, y3: number, t: number, w: number): number {
var t2 = t * t;
var t3 = t2 * t;
var u = (1-w) * 0.5;
// Calcul des fonctions de base d'une spline cardinale
var b0 = -u * t + 2 * u * t2 - u * t3;
var b1 = 1 + (u - 3) * t2 + (2 - u) * t3;
var b2 = u * t + (3 - 2 * u) * t2 + (u - 2) * t3;
var b3 = -u * t2 + u * t3;
return (b0 * y0) + (b1 * y1) + (b2 * y2) + (b3 * y3);
}|
Implémentation de l'interpolation par spline cardinale |
Les paramètres ici sont identiques à la fonction catmullromSpline() vu précédemment, à l'exception du paramètre w qui correspond à la tension aux tangentes. La fonction cardinalSpline() renvoie l'interpolation entre les nœuds correspondant à y1 et y2 suivant t.
8-5. Spline cubique▲
Les splines cubiques présentées jusqu'à présent étaient des splines continûment dérivable une fois (kitxmlcodeinlinelatexdvpC^1finkitxmlcodeinlinelatexdvp). Cependant, le terme de spline cubique sous-entend en général une fonction de classe kitxmlcodeinlinelatexdvpC^2finkitxmlcodeinlinelatexdvp, ayant une dérivée seconde continue et non nulle.
Une continuité de classe kitxmlcodeinlinelatexdvpC^2finkitxmlcodeinlinelatexdvp peut être utile car non seulement plus esthétique, mais pouvant également satisfaire par exemple des contraintes physiques dans le domaine de la conception industrielle :
- la propriété d'une surface non plane à réfléchir la lumière de façon homogène (comme la carrosserie d'une voiture) ou bien,
- la discrétion et les qualités mécaniques d'une jonction entre deux objets assemblés.
Les splines cubiques de classe kitxmlcodeinlinelatexdvpC^2finkitxmlcodeinlinelatexdvp qu'on nommera simplement splines cubiques dans cette section, doivent donc vérifier les propriétés de continuité et de dérivabilité déjà évoquées à la section §8.1.
Étant donné kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp nœuds, la spline cubique ayant pour morceaux les polynômes kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp définis pour les kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp sous-intervalles kitxmlcodeinlinelatexdvp[x_i,x_{i+1}]finkitxmlcodeinlinelatexdvp doit être deux fois continûment dérivable sur kitxmlcodeinlinelatexdvp[x_0,x_n]finkitxmlcodeinlinelatexdvp. Autrement dit les propriétés suivantes doivent être vérifiées :
P1. kitxmlcodeinlinelatexdvpf_i(x_i)=y_ifinkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp compris entre kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn-1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf_{n-1}(x_n)=y_nfinkitxmlcodeinlinelatexdvp.
P2. kitxmlcodeinlinelatexdvpf_i(x_{i+1})=f_{i+1}(x_{i+1})finkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp compris entre kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn-2finkitxmlcodeinlinelatexdvp.
P3. kitxmlcodeinlinelatexdvpf'_i(x_{i+1})=f'_{i+1}(x_{i+1})finkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp compris entre kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn-2finkitxmlcodeinlinelatexdvp.
P4. kitxmlcodeinlinelatexdvpf''_i(x_{i+1})=f''_{i+1}(x_{i+1})finkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp compris entre kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn-2finkitxmlcodeinlinelatexdvp.
Chaque morceau kitxmlcodeinlinelatexdvpf_i(x_i)finkitxmlcodeinlinelatexdvp de la spline est un polynôme de degré 3 et a donc 4 coefficients constants inconnus kitxmlcodeinlinelatexdvpa_{i,0}, a_{i,1}, a_{i,2} et a_{i,3}finkitxmlcodeinlinelatexdvp. Il y a donc kitxmlcodeinlinelatexdvp4nfinkitxmlcodeinlinelatexdvp inconnues à déterminer.
La propriété P1 correspond aux contraintes d'interpolations des nœuds. Elle fournit kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp équations.
Les propriétés P2, P3 et P4 correspondent aux différents niveaux de continuité souhaités. Elles fournissent pour chacune d'elles kitxmlcodeinlinelatexdvpn-1finkitxmlcodeinlinelatexdvp équations et non pas kitxmlcodeinlinelatexdvpn+1finkitxmlcodeinlinelatexdvp équation à cause des deux nœuds aux extrémités en kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp qui ne sont pas concernés par la continuité.
Ces équations sous une forme développée donnent ceci :
kitxmlcodelatexdvp\begin{array}{l} \text{(P1)}\begin{cases} a_{0,0}+&a_{0,1}x_0+&a_{0,2}x_0^2+&a_{0,3}x_0^3&=y_0\\ a_{1,0}+&a_{1,1}x_1+&a_{1,2}x_1^2+&a_{1,3}x_1^3&=y_1\\ …\\ a_{n,0}+&a_{n,1}x_n+&a_{n,2}x_n^2+&a_{n,3}x_n^3&=y_n \end{cases}\\\\ \text{(P2)}\begin{cases} a_{0,0}+&a_{0,1}x_1+&a_{0,2}x_1^2+&a_{0,3}x_1^3&=a_{1,0}+&a_{1,1}x_1+&a_{1,2}x_1^2+&a_{1,3}x_1^3\\ a_{1,0}+&a_{1,1}x_2+&a_{1,2}x_2^2+&a_{1,3}x_2^3&=a_{2,0}+&a_{2,1}x_2+&a_{2,2}x_2^2+&a_{2,3}x_2^3\\ …\\ a_{n-2,0}+&a_{n-2,1}x_{n-1}+&a_{n-2,2}x_{n-1}^2+&a_{n-2,3}x_{n-1}^3&=a_{n-1,0}+&a_{n-1,1}x_{n-1}+&a_{n-1,2}x_{n-1}^2+&a_{n-1,3}x_{n-1}^3 \end{cases}\\\\ \text{(P3)}\begin{cases} a_{0,1}+&2a_{0,2}x_1+&3 a_{0,3}x_1^2&=a_{1,1}+&2a_{1,2}x_1+&3a_{1,3}x_1^2\\ a_{1,1}+&2a_{1,2}x_2+&3 a_{1,3}x_2^2&=a_{2,1}+&2a_{2,2}x_2+&3a_{2,3}x_2^2\\ …\\ a_{n-2,1}+&2a_{n-2,2}x_{n-1}+&3a_{n-2,3}x_{n-1}^2&=a_{n-1,1}+&2a_{n-1,2}x_{n-1}+&3a_{n-1,3}x{n-1}^2 \end{cases}\\\\ \text{(P4)}\begin{cases} 2a_{0,2}+&6a_{0,3}x_1&=2a_{1,2}+&6a_{1,3}x_1\\ 2a_{1,2}+&6a_{1,3}x_2&=2a_{2,2}+&6a_{2,3}x_2\\ …\\ 2a_{n-2,2}+&6a_{n-2,3}x_{n-1}&=2a_{n-1,2}+&6a_{n-1,3}x_{n-1} \end{cases} \end{array}finkitxmlcodelatexdvpNous avons ainsi kitxmlcodeinlinelatexdvp(n+1)+3(n-1)=4n-2finkitxmlcodeinlinelatexdvp équations pour kitxmlcodeinlinelatexdvp4nfinkitxmlcodeinlinelatexdvp inconnues. Pour avoir une solution unique, il nous manque 2 équations concernant chacune des deux extrémités en kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpx_nfinkitxmlcodeinlinelatexdvp. Ces équations peuvent être définies selon l'aspect souhaité aux extrémités. On distingue généralement deux grandes familles de splines cubiques, même si de nombreuses variantes ont été imaginées :
- La spline naturelle (natural spline). A défaut de connaître la première ou la seconde dérivée aux extrémités, on peut poser kitxmlcodeinlinelatexdvpf''(x_0)=0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf''(x_n)=0finkitxmlcodeinlinelatexdvp.
- La spline encastrée (clamped spline) lorsque la valeur de la dérivée première aux extrémités est non nulle.
Une fois qu'on a bien kitxmlcodeinlinelatexdvp4nfinkitxmlcodeinlinelatexdvp équations pour kitxmlcodeinlinelatexdvp4nfinkitxmlcodeinlinelatexdvp inconnues, on obtient un système linéaire pouvant s'exprimer sous la forme d'une matrice inversible.
Cependant, inverser naïvement une telle matrice, en utilisant par exemple la méthode du pivot de Gauss dont la complexité est en kitxmlcodeinlinelatexdvpO(n^3)finkitxmlcodeinlinelatexdvp, n'est pas plus enviable que de résoudre un système de Vandermonde dans le cas de l'interpolation polynomiale globale.
En choisissant utilisant une telle matrice nous perdrions l'avantage semi-locale des splines puisque pour déterminer coefficients d'un seul morceau de la spline, nous devrions prendre en compte la totalité des nœuds.
Heureusement, il est possible de réarranger et simplifier ce système pour aboutir à un système tridiagonal qui peut être résolu en une complexité kitxmlcodeinlinelatexdvpO(n)finkitxmlcodeinlinelatexdvp.
Les calculs qui vont suivre ont pour but d'expliciter l'obtention de ce système tridiagonal.
Chaque morceau kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp étant un polynôme de degré 3, par conséquent la dérivé seconde kitxmlcodeinlinelatexdvpf''_i(x)finkitxmlcodeinlinelatexdvp est un polynôme linéaire de degré 1 qui peut s'écrire comme une interpolation linéaire lagrangienne entre kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpx_{i+1}finkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpf''_i(x)=\frac{f''_i(x_i) (x-x_{i+1})}{(x_i-x_{i+1})}+\frac{f''_{i+1}(x-x_i)}{(x_{i+1}-x_i)}finkitxmlcodelatexdvpCette formule peut se réécrire en posant kitxmlcodeinlinelatexdvpm_i=f''_i(x_i)finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvph=x_{i+1}-x_ifinkitxmlcodeinlinelatexdvp, où kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp désigne le « pas » qui est ici constant et non nul comme c'est le cas depuis le début de ce document où on se donne des points initiaux équirépartis. On obtient alors :
kitxmlcodelatexdvpf''_i(x)=\frac{m_i}{h}(x-x_{i+1})+\frac{m_{i+1}}{h}(x-x_i)finkitxmlcodelatexdvpEn intégrant deux fois la dérivée seconde pour revenir au polynôme interpolateur on obtient l'expression suivante :
kitxmlcodelatexdvpf_i(x)=A_i(x_{i+1}-x)^3+B_i (x-x_i)^3+C_i (x_{i+1}-x)+D_i(x-x_i)finkitxmlcodelatexdvp kitxmlcodelatexdvp\text{avec} \begin{cases} A_i=\frac{\displaystyle m_i}{\displaystyle 6h}\\\\ B_i=\frac{\displaystyle m_{i+1}}{\displaystyle 6h}\\\\ C_i=\frac{\displaystyle y_i}{\displaystyle h} - \frac{\displaystyle hm_i}{\displaystyle 6}\\\\ D_i=\frac{\displaystyle y_{i+1}}{\displaystyle h} - \frac{\displaystyle hm_{i+1}}{\displaystyle 6} \end{cases}finkitxmlcodelatexdvpLes coefficients kitxmlcodeinlinelatexdvpA_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpB_ifinkitxmlcodeinlinelatexdvp ne sont qu'une simplification de la notation, tandis que kitxmlcodeinlinelatexdvpC_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpD_ifinkitxmlcodeinlinelatexdvp sont les constantes d'intégration résolues en utilisant les conditions d'interpolation kitxmlcodeinlinelatexdvpf_i(x_i)=y_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf_i(x_i+1)=y_i+1finkitxmlcodeinlinelatexdvp (propriété P1).
Il ne nous manque que les valeurs kitxmlcodeinlinelatexdvpm_ifinkitxmlcodeinlinelatexdvp pour connaître kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp. Pour obtenir ces valeurs, nous pouvons dériver la nouvelle expression de kitxmlcodeinlinelatexdvpf_i(x)finkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpf'_i(x)=-3A_i(x_{i+1}-x)^2+3B_i(x-x_i)^2-C_i+D_ifinkitxmlcodelatexdvpL'évaluation de kitxmlcodeinlinelatexdvpf'_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf'_{i-1}finkitxmlcodeinlinelatexdvp en kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp donne :
kitxmlcodelatexdvp\begin{cases} f'_i(x_i)=-\frac{\displaystyle h}{\displaystyle 3}m_i - \frac{\displaystyle h}{\displaystyle 6}m_{i+1} + \frac{\displaystyle y_{i+1}-y_i}{\displaystyle h}\\\\ f'_{i-1}(x_i)=-\frac{\displaystyle h}{\displaystyle 3}m_{i-1} - \frac{\displaystyle h}{\displaystyle 6}m_i + \frac{\displaystyle y_i-y_{i-1}}{\displaystyle h}\\ \end{cases}finkitxmlcodelatexdvpEn faisant appel à la propriété P3, on en déduit :
kitxmlcodelatexdvphm_{i-1}+4hm_i+hm_{i+1}=u_ifinkitxmlcodelatexdvpavec kitxmlcodeinlinelatexdvpu_i=\frac{6}{h}(y_{i-1}-2y_i+y_{i+1})finkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp compris entre kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn-2finkitxmlcodeinlinelatexdvp.
De là, nous pouvons en déduire le système tridiagonal associé :
kitxmlcodelatexdvph \begin{pmatrix} 4 & 1 & & \dots & 0 & 0 & 0\\ 1 & 4 & 1 & \dots & 0 & 0 & 0\\ 0 & 1 & 4 & \dots & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots\\ 0 & 0 & 0 &\dots & 4 & 1 & 0\\ 0 & 0 & 0 &\dots & 1 & 4 & 1\\ 0 & 0 & 0 &\dots & 0 & 1 & 4\\ \end{pmatrix} \begin{pmatrix} m_1\\ m_2\\ m_3\\ \vdots\\ m_{n-3}\\ m_{n-2}\\ m_{n-1}\\ \end{pmatrix} = \begin{pmatrix} u_1\\ u_2\\ u_3\\ \vdots\\ u_{n-3}\\ u_{n-2}\\ u_{n-1}\\ \end{pmatrix}finkitxmlcodelatexdvp